

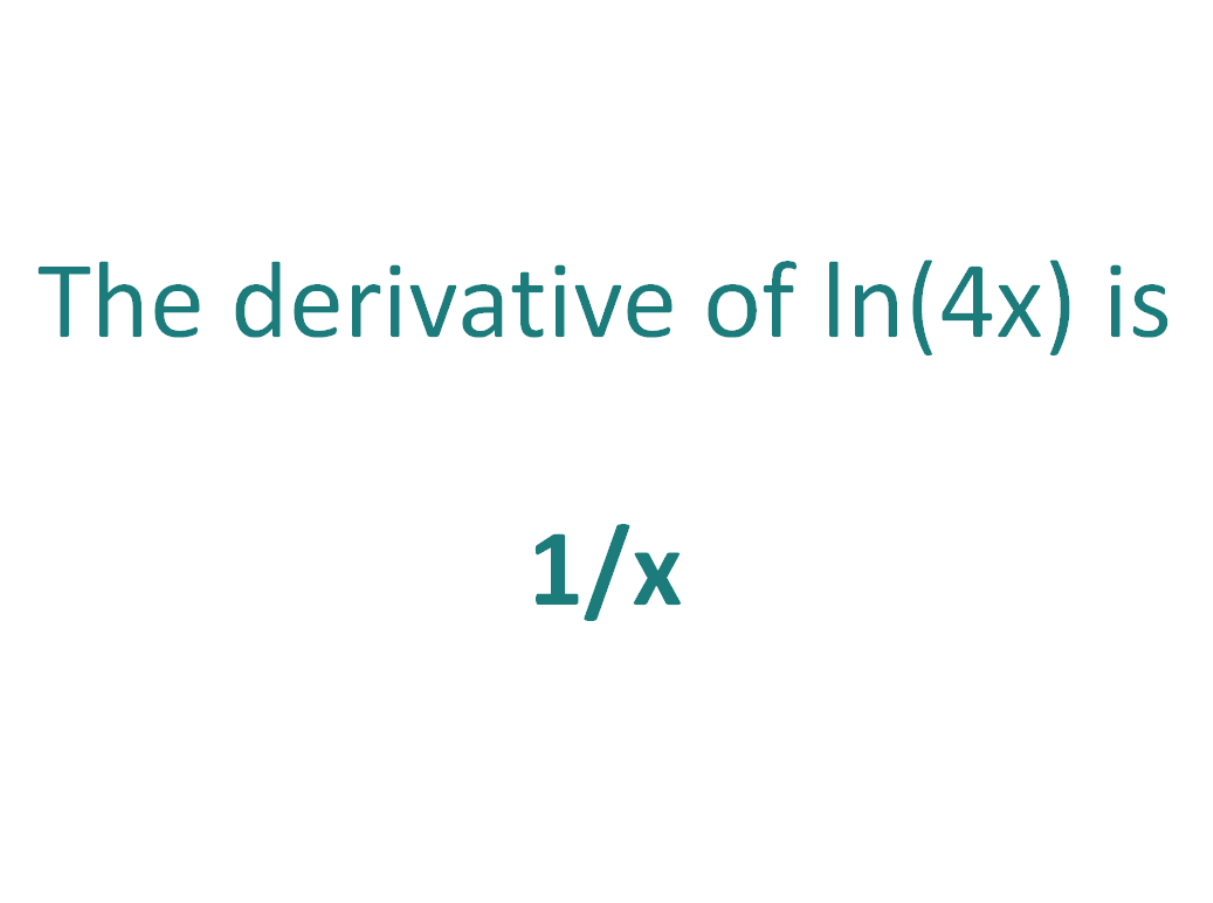
N: int, alternate order of derivation.Its default Value is 1. Print ("Etymology of expression with respect to x: SYNTAX: The Average Rate of Change Formula calculates the slope of a line or a curve on a given range.Ī(x) = f(b)-f(a) /(b-a) Rules of Derivatives:ġ- If f(x)=c, where c is constant,then f ‘(x)=0Ģ-If f(x)=x^n,where n is real number, then f ‘(x) =n x^n-1ģ- So the Product rule is: Suppose the function u=f(x) and v=g(x) Then, d(uv)/dx =udv/dx+vdu/dx Application of partial derivative:ĭerivatives in chemistry: One use of derivatives in chemistry is when we want to Solve that the concentration of an element in a product.ĭerivative(expression, reference variable) Differentiating logarithmic functions using log properties.

Practice: Differentiate logarithmic functions. ‘dx’ does not mean that d times x and ‘dy’ does not mean that d times y.ĭy/dx does not mean dy/ dx. Derivatives of sin (x), cos (x), tan (x), e & ln (x) Derivative of logx (for any positive base a1) Worked example: Derivative of log (x+x) using the chain rule. Functions on closed intervals must have one-sided derivatives defined at the endpoints. Note for second-order derivatives, the notation is often used. We can use the above property to find the derivative for the logarithmic function. Note: If two functions are inverses of each other then, It is a known fact that natural exponential and natural log are the inverses of each other. These are called higher-order derivatives. Notice the fact that these functions are actually inverses of each other. When a derivative is taken times, the notation or is used. Note: we know that f ‘(x) said that “f is prime of x” Important notes:Ī function is different if it is derived everywhere in its domain. Given a function, there are many ways to denote the derivative of with respect to. After that, the Derivative tells us the slope of the function at any point. Differentiation is also known as the process to find the rate of change. The fundamental theorem states that anti-discrimination is similar to integration. The process of finding a derivative of a function is Known as differentiation. Thus, it is true for any function that the logarithmic derivative of a product is the sum of the logarithmic derivatives of the factors (when they are defined).
HOW TO FIND DERIVATIVE OF LOG FUNCTION HOW TO
Also, we will see how to calculate derivative functions in Python. (In fact, these properties are why we call these functions “natural” in the first place!)įrom these, we can use the identities given previously, especially the base-change formula, to find derivatives for most any logarithmic or exponential function.In this tutorial, we will learn about Derivative function, the rate of change of a quantity y with respect to another quantity x is called the derivative or differential coefficient of y with respect to x. I have to compute fractional-order derivative and integral of natural logarithmic function, log(t). Look at some of the basic ways we can manipulate logarithmic functions: This means that there is a “duality” to the properties of logarithmic and exponential functions. Take a moment to look over that and make sure you understand how the log and exponential functions are opposites of each other. In general, the logarithm to base b, written \(\log_b x\), is the inverse of the function \(f(x)=b^x\).
Therefore, the natural logarithm of x is defined as the inverse of the natural exponential function: For example log base 10 of 100 is 2, because 10 to the second power is 100. When we take the logarithm of a number, the answer is the exponent required to raise the base of the logarithm (often 10 or e) to the original number. Remember that a logarithm is the inverse of an exponential. We'll see one reason why this constant is important later on. 1.) Find the derivative y0 of: y ln(x4 sin2 x) We can use the log laws to simplify before di erentiating: y ln(x4 sin2 x) ln(x4) + ln(sin2 x) 4ln(x) + 2ln(sinx) Now that we have simpli ed y, we take the derivative: y0 4 1 x + 2 1 sinx cosx We can simplify this somewhat: y0 4 x + 2cotx 2.) Find the derivative y0 of: y p xex2(x2 + 1)10 This is a very nasty function. The natural exponential function is defined as Review of Logarithms and Exponentialsįirst, let's clarify what we mean by the natural logarithm and natural exponential function. While there are whole families of logarithmic and exponential functions, there are two in particular that are very special: the natural logarithm and natural exponential function. In this lesson, we'll see how to differentiate logarithmic and exponential functions. Differentiating a Logarithm or Exponentialīy now, you've seen how to differentiate simple polynomial functions, and perhaps a few other special functions (like trigonometric functions).


 0 kommentar(er)
0 kommentar(er)
